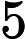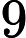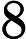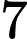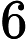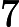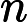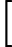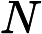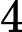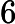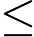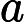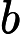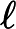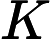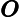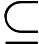Des problèmes en

27

Quels problèmes sont connus pour appartenir à mais ne sont pas connus pour appartenir à ? $\mathsf{BPP}$ $\mathsf P$

Plus précisément, je m'intéresse aux problèmes indépendants , c'est-à-dire dont les dérandomisations ne sont pas connues pour être équivalentes. Par exemple, on sait que la dérandomisation du PIT et la factorisation polynomiale multivariée sont équivalentes et je les considérerais comme un seul problème.

La motivation de ma question est qu'il est courant de dire qu ' "il y a peu de problèmes dans ne sont pas connus pour être en " $\mathsf{BPP}$ $\mathsf{P}$ , mais je n'ai pas pu en trouver la liste. En particulier, si je dois citer des problèmes dans cette catégorie, je cite généralement la factorisation de polynômes univariés sur des champs finis, ou la factorisation de polynômes multivariés. Je suppose qu'il existe des exemples qui ne sont pas liés à la factorisation polynomiale, par exemple dans d'autres domaines tels que la théorie des graphes ou la théorie du langage formel.

PS: Je trouve curieux qu'une question similaire n'existe pas encore sur ce site. Mes excuses si je ne l'ai tout simplement pas trouvé (ou eux)!

derandomization

— Bruno
source

6

Les réponses à ce message contiennent deux exemples cstheory.stackexchange.com/questions/11425/…

— Mohammad Al-Turkistany

13

Si vous demandez des problèmes indépendants, que diriez-vous:

$[N, 5N/4]$
$[N, 9N/8]$
$[N, 17N/16]$
$[N, 33N/32]$
$[N, 65N/64]$
$\ldots$

Il est extrêmement probable que si vous aviez réellement un algorithme polynomial pour résoudre le premier d'entre eux, vous auriez un algorithme polynomial pour chacun d'eux. Mais je ne vois pas comment réduire officiellement l'un de ces éléments à l'un des autres. Bien sûr, le problème

$[N, N+\log^{17} N ]$

résout tout cela.

— Peter Shor
source

Pour être précis, quelle est la version décisionnelle de ces problèmes que vous avez en tête? Merci.

— usul

@usul: Je n'ai pas de version décisionnelle de ces problèmes en tête. Est ce que j'ai besoin de? Je me rends compte que techniquement, BPP se compose uniquement de problèmes de décision. La plupart du temps, les problèmes de décision et les problèmes de fonction sont plus ou moins équivalents, ce qui signifie que vous pouvez considérer uniquement les problèmes de décision sans perte de généralité. Je ne suis pas sûr que ce soit vrai pour cette question, et je ne sais pas si le PO ne se soucie que des problèmes de décision ou non.

— Peter Shor

n

$n$

[N, 5 N / 4]

$[N,5N/4]$

[N, 5 N / 4]

$[N, 5N/4]$

N > 10^{6}

$N > 10^6$

N \leq 10^{6}

$N \leq 10^6$

a, b

$a,b$

[a, b]

$[a,b]$

10

$(2^\ell)$

Cela dit, je ne peux penser qu'à deux cas où cette utilisation entraînerait une différence entre BPP et P.

Le premier est l'algorithme récent pour les deux chemins disjoints les plus courts ( PDF de l'auteur ), Björklund et Husfeldt, ICALP 2014.

$|K|=O(\log n)$ $|K|$

— Magnus Wahlström
source

8

Je ne suis pas un expert, mais peut-être que certains exemples (pas si naturels?) Peuvent être directement dérivés en utilisant la technique de réduction déterministe des problèmes de recherche BPP en problèmes de décision BPP , présentée dans:

Oded Goldreich, dans un monde de P = BPP. Études sur la complexité et la cryptographie 2011: 191-232

$(R_{yes},R_{no})$ $R$ $R_{yes} \subseteq R \subseteq (\{0, 1\}^∗ \times \{0, 1\}^∗) \setminus R_{no}$ $R$ $\Pi$ $(R_{yes},R_{no})$ $\Pi$ $(R_{yes},R_{no})$

Le théorème peut être étendu à des problèmes généraux de construction, par exemple (voir Corollaire 3.9 ) considérer le problème de trouver un nombre premier dans un intervalle suffisamment grand:

$c > 7/12$ $N$ $[N, N + N^c]$

L'algorithme randomisé s'exécute dans le temps polynomial attendu; aucun algorithme de temps polynomial déterministe n'est connu; mais si BPP = P, un tel algorithme de temps polynomial déterministe doit exister (car il peut être réduit à un problème de décision BPP).

— Marzio De Biasi
source