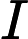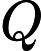Existe-t-il des problèmes connus dans (et non dans ) qui ne sont pas terminés? Je crois comprendre qu'il n'y a actuellement aucun problème connu dans ce cas, mais cela n'a pas été exclu comme une possibilité.
S'il y a un problème qui est (et non ) mais pas , est-ce le résultat de l'absence d'isomorphisme existant entre les instances de ce problème et l'ensemble ? Dans ce cas, comment saurions-nous que le problème n'est pas plus difficile que ce que nous identifions actuellement comme l'ensemble ?