Quelles sont les idées principales, c'est-à-dire les concepts liés au théorème de Bayes ? Je ne demande aucune déduction de la notation mathématique complexe.
Qu'est-ce que le théorème de Bayes?
Réponses:
Le théorème de Bayes est un résultat relativement simple mais fondamental de la théorie des probabilités qui permet de calculer certaines probabilités conditionnelles. Les probabilités conditionnelles ne sont que les probabilités qui reflètent l'influence d'un événement sur la probabilité d'un autre.
En termes simples, dans sa forme la plus connue, il est écrit que la probabilité d’une hypothèse à partir de nouvelles données ( P (H | D) , appelée probabilité postérieure) est égale à l’équation suivante: la probabilité des données observées à partir de l’hypothèse ( P (D | H) , appelée probabilité conditionnelle), multipliée par la probabilité que la théorie soit vraie avant de nouvelles preuves ( P (H) ; appelée probabilité initiale de H), divisée par la probabilité de voir ces données, période ( P (D ), appelée la probabilité marginale de D).
Formellement, l'équation ressemble à ceci:
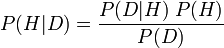
La signification du théorème de Bayes est en grande partie due à son utilisation appropriée qui est un point de discorde entre les écoles de pensée sur les probabilités. Bayesien subjectif (qui interprète la probabilité comme un degré subjectif de conviction), le théorème de Bayes constitue la pierre angulaire des tests théoriques, de la sélection théorique et d'autres pratiques, en intégrant leurs jugements de probabilité subjectifs dans l'équation et en les suivant. Pour un fréquentiste (qui interprète la probabilité comme des fréquences relatives limitantes ), cette utilisation du théorème de Bayes est un abus, et ils s'efforcent plutôt d'utiliser des priors significatifs (non subjectifs) (comme le font les bayésiens objectifs sous une autre interprétation de la probabilité).
Je suis désolé, mais il semble y avoir une certaine confusion ici: le théorème de Bayes n’est pas sujet à une discussion sur le débat interminable Bayesian- Frequentist . C'est un théorème qui correspond aux deux courants de pensée (étant donné qu'il est cohérent avec les axiomes de probabilité de Kolmogorov).
Bien entendu, le théorème de Bayes est au cœur de la statistique bayésienne, mais le théorème lui-même est universel. L’affrontement entre les fréquentistes et les bayésiens a principalement trait à la manière dont les distributions antérieures peuvent être définies ou non.
Donc, si la question concerne le théorème de Bayes (et non les statistiques bayésiennes):
Le théorème de Bayes définit la manière dont on peut calculer des probabilités conditionnelles spécifiques. Imaginez, par exemple, que vous connaissiez: la probabilité qu'une personne présente le symptôme A, étant donné qu'elle est atteinte de la maladie X p (A | X); la probabilité qu'une personne en général ait la maladie X p (X); la probabilité que quelqu'un en général présente le symptôme Ap p (A). Avec ces 3 informations, vous pouvez calculer la probabilité qu'une personne soit atteinte de la maladie X, étant donné qu'elle a le sympotisme A p (X | A).
Le théorème de Bayes est un moyen de convertir une probabilité conditionnelle en une autre probabilité conditionnelle P ( B | A ) .
Une pierre d'achoppement pour certains est la signification de . C'est un moyen de réduire l'espace d'événements possibles en considérant uniquement les événements où A se produit (ou est vrai). Ainsi, par exemple, la probabilité qu'un dé lancé, juste, atterrit sur six, P (sur 6 ) , est de 1/6, mais la probabilité qu'un dé atterrit sur six alors qu'il a atteint un nombre pair, P (sur 6, | dés débarque même ) , est 1/3.
Vous pouvez dériver le théorème de Bayes vous-même comme suit. Commencez avec la définition du ratio d'une probabilité conditionnelle:
et hop!
En ce qui concerne l’intérêt de faire pivoter une probabilité conditionnelle de cette manière, considérons l’exemple courant qui consiste à essayer de déduire la probabilité qu’une personne ait une maladie compte tenu de son symptôme, c’est-à-dire que nous savons qu’elle en a un - nous pouvons simplement le voir - mais nous ne pouvons pas être sûrs qu’ils soient atteints et devons en déduire. Je vais commencer par la formule et revenir en arrière.
Donc, pour résoudre ce problème, vous devez connaître la probabilité antérieure du symptôme, la probabilité antérieure de la maladie (c.-à-d. Quelle est la fréquence ou la rareté du symptôme et de la maladie) et également la probabilité que quelqu'un présente un symptôme, car nous savons que quelqu'un en a une maladie (par exemple, via des tests de laboratoire coûteux et fastidieux).
Cela peut devenir beaucoup plus compliqué que cela, par exemple si vous avez plusieurs maladies et symptômes, mais l'idée est la même. Plus généralement encore, le théorème de Bayes apparaît souvent si vous avez une théorie de la probabilité des relations entre les causes (par exemple, les maladies) et les effets (par exemple, les symptômes) et que vous devez raisonner à l'envers (par exemple, vous voyez certains symptômes dont vous voulez déduire la maladie sous-jacente).
Il existe deux principales écoles de pensée: la statistique fréquentiste et la méthode bayésienne .
Le théorème de Bayes est lié à ce dernier point et peut être perçu comme un moyen de comprendre comment la probabilité qu'une théorie soit vraie est affectée par un nouvel élément de preuve. Ceci est connu sous le nom de probabilité conditionnelle. Vous voudrez peut-être examiner cela pour avoir une idée du calcul.
Laissez-moi vous donner un aperçu très très intuitif. Supposons que vous lancez une pièce 10 fois et que vous obteniez 8 têtes et 2 queues. La question qui vous vient à l’esprit est de savoir si cette pièce a un parti pris pour les têtes ou non.
Maintenant, si vous utilisez des définitions conventionnelles ou une approche fréquentiste de la probabilité, vous pourriez dire que la pièce est non biaisée et qu’il s’agit d’un événement exceptionnel. Par conséquent, vous concluez que la possibilité d'obtenir une tête au tirage au sort est également de 50%.
Mais supposons que vous soyez bayésien. Vous pensez en fait que puisque vous avez un nombre exceptionnellement élevé de têtes, la pièce a un biais sur le côté de la tête. Il existe des méthodes pour calculer ce biais possible. Vous les calculeriez et lorsque vous lanceriez la pièce la prochaine fois, vous appelleriez certainement une tête.
Ainsi, la probabilité bayésienne concerne la croyance que vous développez en fonction des données que vous observez. J'espère que c'était assez simple.
Le théorème de Bayes relie deux idées: probabilité et vraisemblance. La probabilité dit: compte tenu de ce modèle, voici les résultats. Donc, avec une pièce équitable, j'aurai des têtes 50% du temps. La probabilité indique: compte tenu de ces résultats, voici ce que nous pouvons dire sur le modèle. Donc: si vous lancez une pièce de monnaie 100 fois et obtenez 88 têtes (pour reprendre un exemple précédent et le rendre plus extrême), alors la probabilité que le modèle de pièce de monnaie soit correct est correcte n'est pas si élevée.
L'un des exemples standard utilisés pour illustrer le théorème de Bayes est l'idée de tester une maladie: si vous faites un test précis à 95% pour une maladie qui touche 1 personne sur 1000 dans la population et que votre test est positif, quelles sont les chances que vous avez la maladie?
La réponse naïve est de 95%, mais cela ne tient pas compte du fait que 5% des tests sur 9999 personnes sur 10000 donneront un faux positif. Donc, vos chances d'avoir la maladie sont bien inférieures à 95%.
Mon utilisation de l'expression vague "quelles sont les chances" est délibérée. Pour utiliser le langage probabilité / vraisemblance: la probabilité que le test soit précis est de 95%, mais ce que vous voulez savoir, c'est la probabilité que vous soyez atteint de la maladie.
Un peu hors sujet: L'autre exemple classique que le théorème de Bayes est utilisé pour résoudre dans tous les manuels est le problème de Monty Hall: vous êtes dans un jeu télévisé. Il y a un prix derrière l'une des trois portes. Vous choisissez la porte une. L'hôte ouvre la porte trois pour révéler aucun prix. Devriez-vous passer à la porte deux si vous en avez l'occasion?
J'aime la reformulation de la question (avec la référence ci-dessous): vous êtes dans un jeu télévisé. Il y a un prix derrière l'une des millions de portes. Vous choisissez la porte une. L'hôte ouvre toutes les autres portes, à l'exception de la porte 104632, sans révéler aucun prix. Devriez-vous changer pour la porte 104632?
Mon livre préféré, qui traite du théorème de Bayes, du point de vue bayésien, est "Théorie de l'information, algorithmes d'inférence et d'apprentissage", de David JC MacKay. C'est un livre de la Cambridge University Press, ISBN-13: 9780521642989. Ma réponse est (j'espère) un résumé du genre de discussions qui ont été faites dans le livre. (Les règles habituelles s'appliquent: je n'ai aucune affiliation avec l'auteur, j'aime juste le livre).
Le théorème de Bayes dans sa forme la plus évidente est simplement une reformulation de deux choses:
Donc, en utilisant la symétrie:
Alors c'est ça? Comment une chose aussi simple peut-elle être si géniale? Comme pour la plupart des choses "c'est le voyage qui est plus important que la destination". Le théorème de Bayes bascule à cause des arguments qui y ont conduit.
Ce qui manque à cela, c'est que la règle de produit et la règle de somme
Maintenant, la "règle" dans la logique déductive est que si vous avez une relation "A implique B", alors vous avez aussi "Non B implique Non A". Nous avons donc "un raisonnement cohérent implique le théorème de Bayes". Cela signifie "Le théorème de Non Bayes implique un raisonnement non cohérent". c'est-à-dire que si votre résultat n'est pas équivalent à un résultat bayésien pour une certaine probabilité antérieure et probable, vous raisonnerez de manière incohérente.
Ce résultat est appelé le théorème de Cox et a été prouvé dans "Algèbre de l'inférence probable" dans les années 1940. Une dérivation plus récente est donnée dans la théorie de la faisabilité: La logique de la science.
J'aime beaucoup l'introduction de Kevin Murphy dans le théorème de Bayes http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html
La citation ici est tirée d'un article d'économiste:
http://www.cs.ubc.ca/~murphyk/Bayes/economist.html
L'approche bayésienne consiste essentiellement à fournir une règle mathématique expliquant comment vous devez modifier vos croyances existantes à la lumière de nouvelles preuves. En d'autres termes, cela permet aux scientifiques de combiner de nouvelles données avec leurs connaissances ou leurs compétences existantes. L'exemple canonique est d'imaginer qu'un nouveau-né précoce observe son premier coucher de soleil et se demande si le soleil se lèvera ou non. Il assigne des probabilités antérieures égales aux deux résultats possibles et le représente en plaçant une bille blanche et une noire dans un sac. Le lendemain, quand le soleil se lève, l'enfant place une autre bille de marbre blanc dans le sac. La probabilité qu’une bille prélevée au hasard dans le sac devienne blanche (c’est-à-dire le degré de confiance de l’enfant en levers de soleil futurs) est ainsi passée de la moitié à deux tiers. Après le lever du soleil le lendemain, l'enfant ajoute une autre bille blanche et la probabilité (et donc le degré de croyance) va des deux tiers aux trois quarts. Etc. Peu à peu, la croyance initiale selon laquelle le soleil risque tout autant de ne pas se lever chaque matin est modifiée pour devenir une quasi-certitude que le soleil se lève toujours.