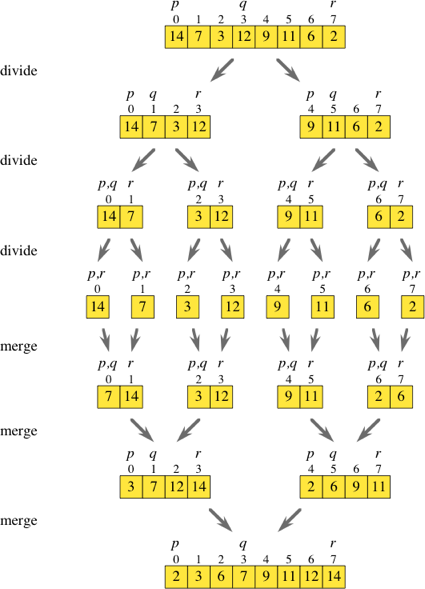
Peut-on éviter l'étape de «division» dans un tri par fusion?

Tri par fusion

Le tri par fusion est donc un algorithme de division et de conquête. Pendant que je regardais le diagramme ci-dessus, je me demandais s'il était possible de contourner fondamentalement toutes les étapes de division.

Si vous parcourez le tableau d'origine en sautant de deux, vous pouvez obtenir les éléments à l'index i et i + 1 et les placer dans leurs propres tableaux triés. Une fois que vous avez tous ces sous-tableaux ([7,14], [3,12], [9,11] et [2,6] comme indiqué dans le diagramme), vous pouvez simplement continuer avec la routine de fusion normale pour obtenir un tableau trié.

L'itération à travers la baie et la génération immédiate des sous-baies requises sont-elles moins efficaces que l'exécution des étapes de division dans leur intégralité?

— Jimmy_Rustle
source

Connexe: cs.stackexchange.com/questions/77075/…

— Omar

Réponses:

La confusion provient de la différence entre la description conceptuelle de l'algorithme et sa mise en œuvre .

Le tri par fusion logique est décrit comme la division du tableau en plus petits tableaux, puis leur fusion à nouveau. Cependant, "diviser le tableau" n'implique pas "créer un tableau entièrement nouveau en mémoire", ou quelque chose comme ça - il pourrait être implémenté dans le code comme

/*
 * Note: array is now split into  [0..n) and [n..N)
 */

c'est-à-dire qu'aucun travail réel n'a lieu, et le "fractionnement" est purement conceptuel. Donc, ce que vous suggérez fonctionne certainement, mais logiquement, vous "divisez" toujours les tableaux - vous n'avez tout simplement pas besoin de travail sur l'ordinateur pour le faire :-)

— psmears
source

Personnellement, j'aime vraiment le tri de fusion ascendant car il est plus simple à implémenter de manière à éviter d'allouer un tampon temporaire à chaque niveau de récursivité. Au lieu de cela, vous allouez un tampon une fois et faites un ping-pong entre eux.

— ratchet freak

Cette - la division est un calcul sans opération ... plus la suggestion des OP n'est qu'une introduction d'un équivalent à une fusion de tableaux à élément unique, et commence à utiliser la fusion à partir de la 2e étape, ce qui semble redondant, car la fusion originale fonctionne tout aussi bien. Il ne sert à rien d’optimiser cela. Il introduit uniquement des concepts et une logique redondants.

— luk32

@ratchetfreak: J'adore ça aussi, mais malheureusement ce n'est pas équivalent à top-down (au moins la version que je connais). Il fera la fusion différemment, en arrondissant essentiellement à la prochaine longueur de tableau de puissance de 2, qui, je pense, pourrait même être un peu plus lente. Connaissez-vous une version ascendante qui fait exactement la même fusion sans payer un coût élevé ailleurs?

— user541686

@Mehrdad le seul vrai problème est la petite queue qui doit être fusionnée. Dans le pire des cas, cela signifie une autre passe à fusionner en un seul élément pour les tableaux de longueur 1<<n+1. Bien que je sois sûr que vous pouvez ajuster les choses pour qu'une queue trop petite soit fusionnée dans un passage inférieur.

— ratchet freak

@psmears "vous n'avez tout simplement pas besoin de travail de l'ordinateur pour le faire" - donc je suppose que le coût de performance de n appels d'une fonction de division récursive (7 appels dans le diagramme d'exemple) est fondamentalement négligeable?

— Jimmy_Rustle

Je suppose que ce que vous voulez dire, c'est l' implémentation ascendante . Dans l'implémentation ascendante, vous commencez à partir d'éléments de cellule unique et vous vous déplacez vers le haut en fusionnant les éléments dans des listes / tableaux triés plus grands. Inversez simplement les flèches de votre figure ci-dessus à partir du tableau du milieu, c'est-à-dire des tableaux à un élément.

En outre, vous souhaiterez peut-être optimiser le tri par fusion en divisant les tableaux jusqu'à ce qu'ils atteignent une taille constante, après quoi vous les triez simplement en utilisant par exemple le tri par insertion.

Sinon, le tri sans division du tableau n'est pas possible. En fait, l'essentiel du tri par fusion consiste à diviser et à trier les sous-réseaux, c'est-à-dire diviser pour mieux régner.

— fade2black
source