Pourquoi ne pas simplement vider les réseaux de neurones et l'apprentissage en profondeur? [fermé]

Problème fondamental avec l'apprentissage en profondeur et les réseaux de neurones en général.

1. Les solutions adaptées aux données d'entraînement sont infinies. Nous n'avons pas d'équation mathématique précise qui ne soit satisfaite que par une seule et que nous pouvons dire généralisant le mieux. Pour parler simplement, nous ne savons pas laquelle se généralise le mieux.

2. L'optimisation des poids n'est pas un problème convexe, nous ne savons donc jamais que nous nous retrouvons avec un minimum global ou local.

Alors pourquoi ne pas simplement vider les réseaux de neurones et chercher à la place un meilleur modèle ML? Quelque chose que nous comprenons et quelque chose qui est cohérent avec un ensemble d'équations mathématiques? Linéaire et SVM n'ont pas ces inconvénients mathématiques et sont entièrement cohérents avec un ensemble d'équations mathématiques. Pourquoi ne pas simplement penser sur les mêmes lignes (pas nécessairement linéaire cependant) et proposer un nouveau modèle ML mieux que les réseaux linéaires et SVM et neuronaux et l'apprentissage en profondeur?

1. Ne pas être en mesure de savoir quelle solution se généralise le mieux est un problème, mais cela ne devrait pas nous dissuader d'utiliser autrement une bonne solution. Les humains eux-mêmes ne savent souvent pas ce qui se généralise le mieux (pensez, par exemple, aux théories unificatrices concurrentes de la physique), mais cela ne nous pose pas trop de problèmes.

2. Il a été démontré qu'il est extrêmement rare que la formation échoue en raison des minimums locaux. La plupart des minimums locaux dans un réseau neuronal profond ont une valeur proche du minimum global, donc ce n'est pas un problème. la source

Mais la réponse plus large est que vous pouvez parler toute la journée de la non-convexité et de la sélection des modèles, et les gens utiliseront toujours les réseaux de neurones simplement parce qu'ils fonctionnent mieux qu'autre chose (au moins sur des choses comme la classification d'images).

Bien sûr, il y a aussi des gens qui soutiennent que nous ne devrions pas trop nous concentrer sur les CNN comme la communauté était concentrée sur les SVM il y a quelques décennies, et continuer à chercher la prochaine grande chose. En particulier, je pense que je me souviens que Hinton a regretté l'efficacité des CNN comme quelque chose qui pourrait entraver la recherche. Article similaire

Comme le soulignent les commentaires sur votre question, beaucoup de gens travaillent à trouver quelque chose de mieux. J'aimerais cependant répondre à cette question en développant le commentaire laissé par @josh

Tous les modèles sont faux mais certains sont utiles (Wiki)

L'énoncé ci-dessus est une vérité générale utilisée pour décrire la nature des modèles statistiques. En utilisant les données dont nous disposons, nous pouvons créer des modèles qui nous permettent de faire des choses utiles telles que l'approximation d'une valeur prédite.

Prenons par exemple la régression linéaire

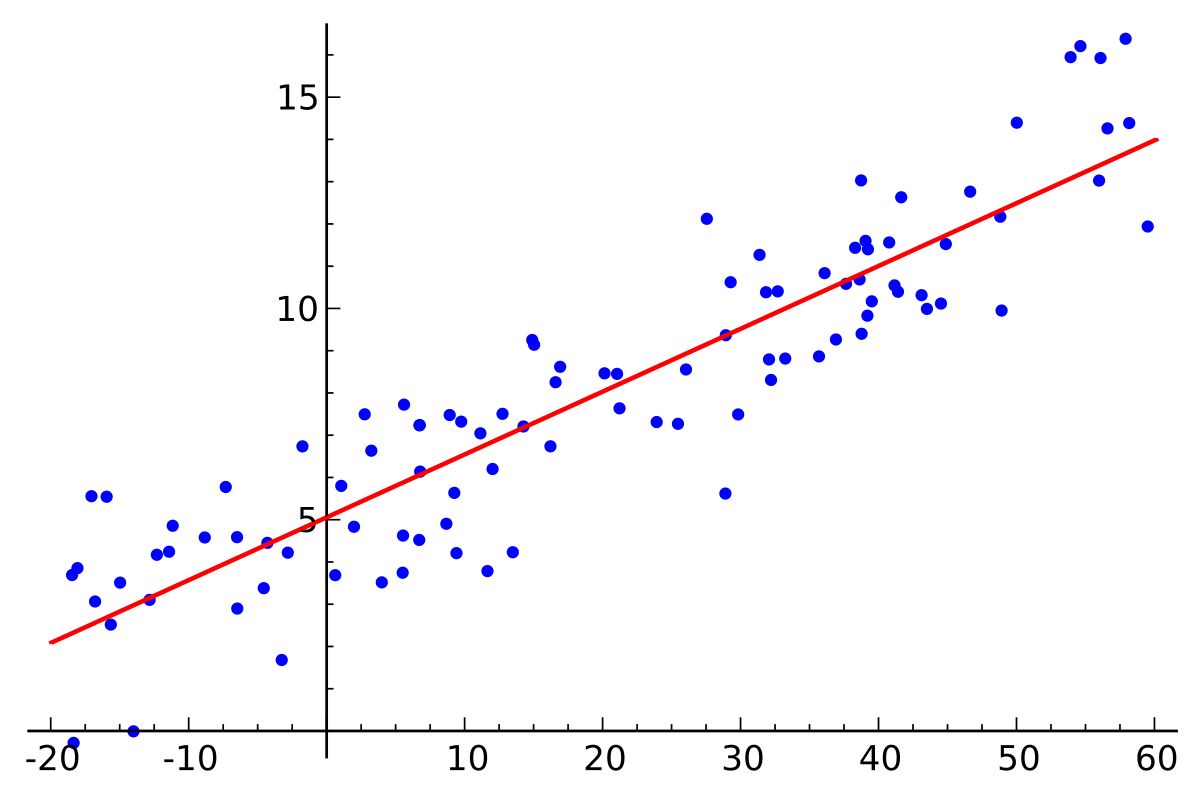
En utilisant un certain nombre d'observations, nous pouvons ajuster un modèle pour nous donner une valeur approximative pour une variable dépendante étant donné toute valeur pour la ou les variables indépendantes.

Burnham, KP; Anderson, DR (2002), Sélection de modèles et multimodèle> Inférence: une approche théorique pratique de l'information (2e éd.):

"Un modèle est une simplification ou une approximation de la réalité et ne reflétera donc pas toute la réalité. ... Box a noté que" tous les modèles sont faux, mais certains sont utiles ". être classé de très utile, utile, quelque peu utile à, enfin, essentiellement inutile.

Les écarts par rapport à notre modèle (comme on peut le voir sur l'image ci-dessus) semblent aléatoires, certaines observations sont en dessous de la ligne et d'autres au-dessus, mais notre ligne de régression montre une corrélation générale. Alors que les écarts dans notre modèle semblent aléatoires, dans des scénarios réalistes, il y aura d'autres facteurs en jeu qui provoquent cet écart. Par exemple, imaginez regarder des voitures pendant qu'elles traversent une intersection où elles doivent tourner à gauche ou à droite pour continuer, les voitures ne tournent pas de façon particulière. Alors que nous pourrions dire que la direction dans laquelle les voitures tournent est complètement aléatoire, chaque conducteur atteint-il la jonction et prend-il à ce moment-là une décision aléatoire de quel sens tourner? En réalité, ils se dirigent probablement vers un endroit spécifique pour une raison spécifique, et sans essayer d'arrêter chaque voiture pour leur demander leur raisonnement, nous ne pouvons que décrire leurs actions comme aléatoires.

Lorsque nous pouvons adapter un modèle avec un écart minimal, dans quelle mesure pouvons-nous être certains qu'une variable inconnue, inaperçue ou incommensurable ne jettera pas à un moment donné notre modèle? Le battement d'ailes d'un papillon au Brésil déclenche-t-il une tornade au Texas?

Le problème avec l'utilisation des modèles linéaires et SVN que vous mentionnez seuls est que nous sommes quelque peu tenus d'observer manuellement nos variables et comment elles s'influencent mutuellement. Nous devons ensuite décider quelles variables sont importantes et écrire un algorithme spécifique à la tâche. Cela peut être simple si nous n'avons que quelques variables, mais qu'en est-il si nous en avions des milliers? Et si nous voulions créer un modèle de reconnaissance d'image généralisé, cela pourrait-il être réalisé de manière réaliste avec cette approche?

L'apprentissage profond et les réseaux de neurones artificiels (RNA) peuvent nous aider à créer des modèles utiles pour d'énormes ensembles de données contenant d'énormes quantités de variables (par exemple des bibliothèques d'images). Comme vous le mentionnez, il existe un nombre incompréhensible de solutions qui pourraient correspondre aux données à l'aide des RNA, mais ce nombre est-il vraiment différent de la quantité de solutions dont nous aurions besoin pour nous développer par essais et erreurs?

L'application des RNA fait une grande partie du travail pour nous, nous pouvons spécifier nos entrées et nos sorties souhaitées (et les ajuster plus tard pour apporter des améliorations) et laisser à l'ANN le soin de trouver la solution. C'est pourquoi les RNA sont souvent décrits comme des "boîtes noires" . À partir d'une entrée donnée, ils produisent une approximation, mais (en termes généraux) ces approximations n'incluent pas de détails sur la façon dont elles ont été approximées.

Et donc, cela revient vraiment au problème que vous essayez de résoudre, car le problème dictera quelle approche de modèle est la plus utile. Les modèles ne sont pas absolument précis et il y a donc toujours un élément d'être «faux», mais plus vos résultats sont précis, plus ils sont utiles. Avoir plus de détails dans les résultats sur la façon dont l'approximation a été faite peut également être utile, selon le problème, il peut même être plus utile qu'une précision accrue.

Si, par exemple, vous calculez le pointage de crédit d'une personne, l'utilisation de la régression et des SVM fournit des calculs qui peuvent être mieux explorés. Il est très utile de pouvoir ajuster le modèle directement et expliquer aux clients l'effet que des variables indépendantes distinctes ont sur leur score global. Un ANN peut aider à traiter de plus grandes quantités de variables pour obtenir un score plus précis, mais cette précision serait-elle plus utile?

Le minimum global peut aussi bien être inutile, donc nous ne nous soucions pas vraiment de le trouver ou non. La raison en est que, pour les réseaux profonds, non seulement le temps nécessaire pour le trouver devient exponentiellement plus long à mesure que la taille du réseau augmente, mais aussi le minimum global correspond souvent à un surajustement de l'ensemble d'entraînement. Ainsi, la capacité de généralisation du DNN (qui nous tient vraiment à cœur) en souffrirait. De plus, nous préférons souvent des minima plus plats correspondant à une valeur plus élevée de la fonction de perte, que des minima plus nets correspondant à une valeur inférieure de la fonction de perte, car le second traitera très mal l'incertitude dans les entrées. Cela devient de plus en plus clair avec le développement du Bayesian Deep Learning. L'optimisation robuste bat très souvent l'optimisation déterministe, lorsqu'elle est appliquée à des problèmes du monde réel où l'incertitude est importante.

Enfin, c'est un fait que les DNN viennent de botter le cul de méthodes telles que XGBoost dans la classification d'images et la PNL. Une entreprise qui doit réaliser un profit grâce à la classification des images les sélectionnera correctement comme modèles à déployer en production ( et investira une somme importante dans l'ingénierie des fonctionnalités, le pipeline de données, etc. mais je m'égare). Cela ne signifie pas qu'ils dominent tout l'environnement ML: par exemple, ils font pire que XGBoost sur les données structurées (voir les derniers gagnants des compétitions Kaggle) et ils semblent ne pas encore faire aussi bien que les filtres à particules sur la modélisation des séries chronologiques. Cependant, certaines innovations très récentes sur les RNN peuvent modifier cette situation.

Je pense que la meilleure façon de réfléchir à cette question passe par le marché concurrentiel. Si vous videz l'apprentissage en profondeur et que vos concurrents l'utilisent, ET que cela fonctionne mieux que ce que vous utilisiez, alors vous serez battu sur le marché.

Je pense que c'est ce qui se passe, en partie, aujourd'hui, c'est-à-dire que l'apprentissage en profondeur semble fonctionner mieux que tout pour tous les problèmes du marché. Par exemple, les traducteurs de langues en ligne utilisant le deep learning sont meilleurs que les approches purement linguistiques utilisées auparavant. Il y a quelques années à peine, ce n'était pas le cas, mais les progrès de l'apprentissage en profondeur ont amené ceux qui avaient l'habitude à occuper des postes de direction sur le marché.

Je continue de répéter «le marché» parce que c'est ce qui est à l'origine de la poussée actuelle du deep learning. Le moment où les affaires trouvent quelque chose d'utile, que quelque chose se répandra. Ce n'est pas nous , le comité, qui avons décidé que l'apprentissage en profondeur devrait être populaire. Ce sont les affaires et la concurrence.

La deuxième partie, c'est qu'en plus du succès réel de ML, il y a aussi la peur de rater le bateau. Beaucoup d'entreprises sont paranoïaques si elles ratent l'IA, elles échoueront en tant qu'entreprises. Cette peur est nourrie par toutes ces maisons de conseil, Gartners, etc., chuchotant aux PDG qu'ils doivent faire de l'IA ou mourir demain.

Personne n'oblige les entreprises à utiliser le deep learning. L'informatique et la R&D sont emballées par un nouveau jouet. Les applaudissements du milieu universitaire, donc cette fête va durer jusqu'à ce que la musique s'arrête, c'est-à-dire jusqu'à ce que l'apprentissage profond cesse de livrer. En attendant, vous pouvez le vider et trouver une meilleure solution.

Il y a d'excellentes réponses, qui tiennent surtout compte de l'utilité des DL et des ANN. Mais je voudrais objecter l'OP d'une manière plus fondamentale, car la question tient déjà pour acquise l'incohérence mathématique des réseaux de neurones.

Tout d'abord, il existe une théorie mathématique derrière (la plupart des modèles de) réseaux de neurones. Vous pourriez également faire valoir que la régression linéaire ne se généralise pas, sauf si le modèle sous-jacent est ... eh bien, linéaire. Dans les algorithmes neuronaux, un modèle est supposé (même s'il n'est pas explicite) et l'erreur d'ajustement est calculée. Le fait que les algorithmes soient modifiés avec diverses heuristiques n'annule pas le support mathématique d'origine. BTW, l'optimisation locale est également une théorie mathématiquement cohérente, et encore moins utile.

Dans cette optique, si les réseaux de neurones ne constituent qu'une classe de méthodes dans l'ensemble de la boîte à outils des scientifiques, quelle est la ligne qui sépare les réseaux de neurones du reste des techniques? En fait, les SVM étaient autrefois considérés comme une classe de NN et ils apparaissent toujours dans les mêmes livres. D'un autre côté, les NN pourraient être considérés comme une technique de régression (non linéaire), peut-être avec une certaine simplification. Je suis d'accord avec l'OP que nous devons rechercher des algorithmes meilleurs, bien fondés et efficaces, que vous les étiquetiez comme NN ou non.

Je suppose que pour certains problèmes, nous nous soucions moins de la rigueur mathématique et de la simplicité, mais plus de son utilité, le statut actuel est que le réseau de neurones est meilleur pour effectuer certaines tâches comme la reconnaissance de formes dans le traitement d'image.

Il y a beaucoup dans cette question. Reprenons ce que vous avez écrit un par un.

Les solutions adaptées aux données d'entraînement sont infinies. Nous n'avons pas d'équation mathématique précise qui ne soit satisfaite que par une seule et que nous pouvons dire généralisant le mieux.

Le fait qu'il existe une infinité de solutions vient du fait que le problème d'apprentissage est un problème mal posé, il ne peut donc pas y en avoir un qui se généralise le mieux. De plus, aucun théorème du déjeuner gratuit, quelle que soit la méthode que nous utilisons, ne peut garantir qu'il est le meilleur dans tous les problèmes d'apprentissage.

Pour parler simplement, nous ne savons pas laquelle se généralise le mieux.

Cette affirmation n'est pas vraiment vraie. Il existe des théorèmes sur la minimisation empirique des risques par Vapnik & Chervonenkis qui relient le nombre d'échantillons, la dimension VC de la méthode d'apprentissage et l'erreur de généralisation. Notez que cela ne s'applique qu'à un ensemble de données donné. Donc, étant donné un ensemble de données et une procédure d'apprentissage, nous connaissons les limites de la généralisation. Notez que, pour différents ensembles de données, il n'y a pas et ne peut pas être la meilleure procédure d'apprentissage en raison de l'absence de théorème de déjeuner gratuit.

L'optimisation des poids n'est pas un problème convexe, nous ne savons donc jamais que nous nous retrouvons avec un minimum global ou local. Alors pourquoi ne pas simplement vider les réseaux de neurones et chercher à la place un meilleur modèle ML?

Ici, il y a peu de choses que vous devez garder à l'esprit. L'optimisation d'un problème non convexe n'est pas aussi simple qu'un problème convexe; c'est vrai. Cependant, la classe des méthodes d'apprentissage qui sont convexes est limitée (régression linéaire, SVMs) et en pratique, elles fonctionnent moins bien que la classe des méthodes non convexes (boosting, CNNs) sur une variété de problèmes. La partie cruciale est donc qu'en pratique les réseaux de neurones fonctionnent mieux. Bien qu'il existe un certain nombre d'éléments très importants qui permettent au bon fonctionnement des réseaux de neurones:

1. Ils peuvent être appliqués à de très grands ensembles de données en raison de la descente de gradient stochastique.
2. Contrairement aux SVM, l'inférence avec des réseaux profonds ne dépend pas de l'ensemble de données. Cela rend les réseaux neuronaux efficaces au moment du test.
3. Avec les réseaux neuronaux, il est possible de contrôler directement leur capacité d'apprentissage (pensez au nombre de paramètres) simplement en ajoutant plus de couches ou en les agrandissant. Ceci est crucial car pour différents jeux de données, vous souhaiterez peut-être des modèles plus grands ou plus petits.

Quelque chose que nous comprenons et quelque chose qui est cohérent avec un ensemble d'équations mathématiques? Linéaire et SVM n'ont pas ces inconvénients mathématiques et sont entièrement cohérents avec un ensemble d'équations mathématiques. Pourquoi ne pas simplement penser sur les mêmes lignes (pas nécessairement linéaire cependant) et proposer un nouveau modèle ML mieux que les réseaux linéaires et SVM et neuronaux et l'apprentissage en profondeur?

Vider des choses qui fonctionnent parce qu'elles ne les comprennent pas n'est pas une bonne direction de recherche. D'un autre côté, faire un effort pour les comprendre est une excellente direction de recherche. De plus, je ne suis pas d'accord avec le fait que les réseaux de neurones sont incompatibles avec les équations mathématiques. Ils sont assez cohérents. Nous savons comment les optimiser et effectuer l'inférence.

Que diriez-vous de visualiser les réseaux de neurones d'un point de vue expérimental? Ce n'est pas parce que nous les avons créés que nous sommes obligés de les comprendre intuitivement. Ou que nous ne sommes pas autorisés à jouer avec eux afin d'avoir une meilleure compréhension de ce qu'ils font.

Voici quelques réflexions que j'ai sur eux:

• Structure: ce sont des hiérarchies. Ils sont comme des arbres qui partagent des intrants. Les racines sont les entrées et les feuilles sont la couche de sortie. Plus le calque est proche des sorties, plus il est pertinent pour elles, plus le niveau d'abstraction qu'il contient (il s'agit plus de l'image que des pixels).
• Fonctionnalité: ils "jouent" avec les données, le modus operandi est d'expérimenter les relations dans les neurones (poids) jusqu'à ce que les choses "cliquent" (la marge d'erreur est acceptable).

Cela correspond à notre façon de penser. C'est même cohérent avec le fonctionnement de la méthode scientifique. Ainsi, en fissurant les réseaux de neurones, nous pouvons également résoudre la question générale de ce que représente la connaissance.

N'oubliez pas, il existe un vaste domaine de recherche qui utilise la modélisation LMs, GLM, multi-niveaux. Dernièrement, les techniques bayésiennes et le hamiltonien Monte Carlo (la communauté STAN est vraiment à l'avant-garde) sont arrivés à maturité et un certain nombre de problèmes résolus par STAN très facilement et n'ont pas vraiment besoin de NN ou de filets profonds. La recherche en sciences sociales, la microéconomie sont deux (grands) exemples de tels domaines qui adoptent Stan rapidement.

Les modèles Stan sont très "lisibles". Les coefficients ont en fait une interprétation distributionnelle postérieure, tout comme les prédictions. Les priors font partie du processus de génération de données et n'ont pas besoin d'être conjugués pour être performants (comme les gibbs). Le modèle adapté à Stan est un délice, il ajuste en fait les paramètres MCMC embêtants automatiquement et sacrément bien et vous avertit lorsque l'exploration est bloquée avec de très belles visualisations.

Si vous ne l'avez pas déjà essayé, voyez des démos stan impressionnantes ici ).

À la fin de la journée, je pense que les gens ne parlent pas tellement de ces choses parce que la recherche dans ce domaine et les problèmes ne sont pas aussi "sexy" / "cool" qu'avec les NN.

Qu'est-ce qui se passe généralement quand il n'y a pas de cohérence mathématique (au moins dans ce cas de réseaux de neurones) ... quand il ne donne pas les résultats souhaités, sur le test, votre patron reviendra et dira ... essayez Drop out (quels poids, quelle couche, combien est votre mal de tête car il n'y a pas de moyen mathématique pour le déterminer), donc après avoir essayé et espérons avoir obtenu une amélioration marginale mais pas la souhaitée, votre patron reviendra et dira pourquoi pas essayer la décroissance du poids (quel facteur?)? et plus tard, pourquoi n'essayez-vous pas ReLU ou une autre activation sur certaines couches, et toujours pas, pourquoi ne pas essayer la «mise en commun maximale»? toujours pas, pourquoi ne pas essayer la normalisation par lots, toujours pas, ou au moins la convergence, mais pas le résultat souhaité, Oh vous êtes dans un minimum local, essayez un programme de rythme d'apprentissage différent, il suffit de changer l'architecture du réseau? et répétez tout ci-dessus dans différentes combinaisons! Gardez-le dans une boucle jusqu'à ce que vous réussissiez!

D'un autre côté, lorsque vous essayez un SVM cohérent, après convergence, si le résultat n'est pas bon, alors d'accord, le noyau linéaire que nous utilisons n'est pas assez bon car les données peuvent ne pas être linéaires, utilisez un noyau de forme différente, essayez un noyau de forme différente si vous avez un pressentiment, sinon, laissez-le, c'est une limitation de SVM.

Ce que je dis, c'est que les réseaux de neurones sont tellement incohérents, que ce n'est même pas faux! Il n'accepte jamais sa défaite! L'ingénieur / concepteur prend la charge, au cas où cela ne fonctionnerait pas comme souhaité.