Qu'est-ce qu'une forme de coin du tracé PCA indique?

Dans leur article sur autoencoders pour la classification texte Hinton et Salakhutdinov démontré l'intrigue produit par 2 dimensions LSA (qui est étroitement liée à la PCA): .

En appliquant l'ACP à des données dimensionnelles légèrement différentes, absolument différentes, j'ai obtenu un tracé similaire: (sauf dans ce cas, je voulais vraiment savoir s'il y avait une structure interne).

Si nous introduisons des données aléatoires dans PCA, nous obtenons un blob en forme de disque, donc cette forme en forme de coin n'est pas aléatoire. Cela signifie-t-il quelque chose en soi?

En supposant que les variables sont positives ou non négatives, les bords du bord ne sont que des points au-delà desquels les données deviendraient respectivement 0 ou négatives. Comme ces données réelles ont tendance à être asymétriques, nous constatons une plus grande densité de points à l'extrémité inférieure de leur distribution et donc une plus grande densité au "point" du coin.

Plus généralement, l'ACP est simplement une rotation des données et les contraintes sur ces données seront généralement visibles dans les principaux composants de la même manière que celle illustrée dans la question.

Voici un exemple utilisant plusieurs variables log-distribuées normalement:

library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

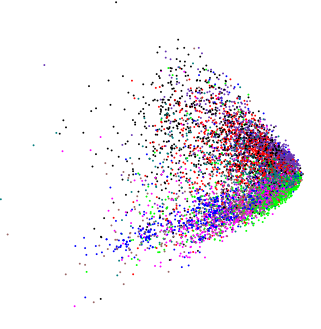
Selon la rotation impliquée par les deux premiers PC, vous pouvez voir le coin ou vous pouvez voir une version quelque peu différente, montrez ici en 3D en utilisant ( ordirgl()à la place de plot())

Ici, en 3D, nous voyons plusieurs pointes dépassant de la masse centrale.

Pour les variables aléatoires gaussiennes ( ) où chacune a la même moyenne et variance, nous voyons une sphère de points$X_i \sim \mathcal(N)(\mu = 0, \sigma = 1)$

set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")

Et pour des variables aléatoires positives uniformes, nous voyons un cube

set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")

Notez qu'ici, à titre d'illustration, je montre l'uniforme en utilisant seulement 3 variables aléatoires, donc les points décrivent un cube en 3D. Avec des dimensions plus élevées / plus de variables, nous ne pouvons pas représenter parfaitement l'hypercube 5d en 3D et la forme distincte du "cube" est donc quelque peu déformée. Des problèmes similaires affectent les autres exemples présentés, mais il est toujours facile de voir les contraintes dans ces exemples.

Pour vos données, une transformation logarithmique des variables avant l'ACP entraînerait la queue et étirerait les données regroupées, tout comme vous pourriez utiliser une telle transformation dans une régression linéaire.

D'autres formes peuvent apparaître dans les parcelles PCA; une telle forme est un artefact de la représentation métrique conservée dans l'APC et est connue sous le nom de fer à cheval . Pour les données avec un gradient long ou dominant (les échantillons disposés le long d'une seule dimension avec des variables augmentant de 0 à un maximum puis diminuant à nouveau à 0 le long de parties des données sont bien connus pour générer de tels artefacts.

ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
                 Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
                 Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
        ylab = "Abundance", xlab = "Sites")

ce qui produit un fer à cheval extrême, où les points aux extrémités des axes se replient au milieu.