Peut-être que l'algorithme lui-même n'est pas si obscur, mais qui peut nommer une implémentation réellement utilisée dans la pratique? Je peux!
TIGCC (un compilateur basé sur GCC pour les calculatrices graphiques TI-89/92 / V200) utilise le tri Shell pour l' qsortimplémentation dans sa bibliothèque standard:
__ATTR_LIB_C__ void qsort(void *list, short num_items, short size, compare_t cmp_func)
{
unsigned short gap,byte_gap,i,j;
char *p,*a,*b,temp;
for (gap=((unsigned short)num_items)>>1; gap>0; gap>>=1) // Yes, this is not a quicksort,
{ // but works fast enough...
byte_gap=gap*(unsigned short)size;
for(i=byte_gap; i<((unsigned short)num_items)*(unsigned short)size; i+=size)
for(p=(char*)list+i-byte_gap; p>=(char*)list; p-= byte_gap)
{
a=p; b=p+byte_gap;
if(cmp_func(a,b)<=0) break;
for(j=size;j;j--)
temp=*a, *a++=*b, *b++=temp;
}
}
}
Le tri du shell a été choisi en faveur de quicksort pour maintenir une taille de code faible. Bien que sa complexité asymptotique soit pire, la TI-89 n'a pas beaucoup de RAM (190K, moins la taille du programme et la taille totale des variables non archivées), il est donc assez sûr de supposer que le nombre d'éléments au dessous de.
Une implémentation plus rapide a été écrite après que je me sois plaint d'être trop lent dans un programme que j'écrivais. Il utilise de meilleures tailles d'espace, ainsi que des optimisations d'assemblage. Il peut être trouvé ici: qsort.c
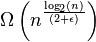 d' exécution pour ϵ > 0.
d' exécution pour ϵ > 0.