Pourquoi le recuit quantique ne peut-il pas être décrit par un modèle de porte?

C'est une question que j'ai eu envie de poser sur la base de cette question , qui note que le recuit quantique est un modèle de calcul entièrement différent du modèle de circuit habituel. J'ai déjà entendu cela, et je crois comprendre que le modèle de porte ne s'applique pas au recuit quantique, mais je n'ai jamais tout à fait compris pourquoi, ni comment analyser les calculs qu'un recuit peut faire. Si je comprends bien à partir de plusieurs exposés (certains par D-wave eux-mêmes!) Le fait que les recuit sont confinés à un hamiltonien spécifique.

Un recuit quantique, tel qu'une machine à ondes D, est une représentation physique du modèle d'Ising et, en tant que tel, a un «problème» hamiltonien de la forme

Essentiellement, le problème à résoudre est mis en correspondance avec l'hamiltonien ci-dessus. Le système commence avec le hamiltonien et le paramètre de recuit, est utilisé pour mapper le hamiltonien initial au problème hamiltonien utilisant .$H_I = \sum_{J=1}^nh'_j\sigma_j^x$$s$$H_I$$H_P$$H\left(s\right) = \left(1-s\right)H_I + sH_P$

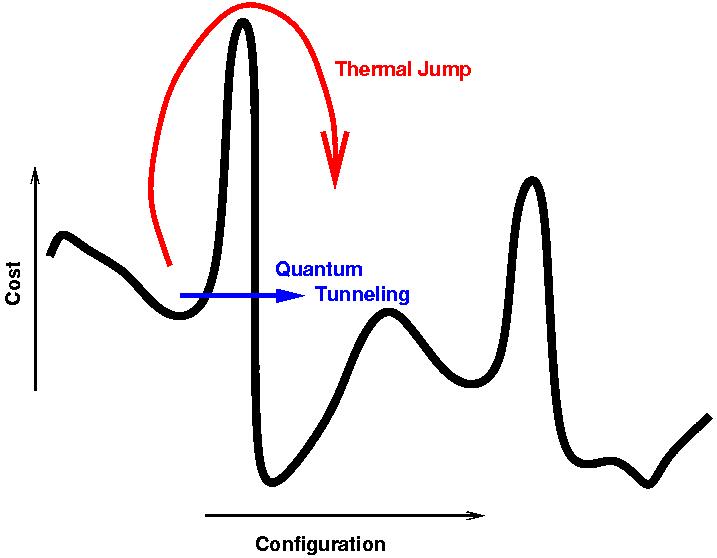
Comme il s'agit d'un recuit, le processus se fait assez lentement pour rester près de l'état fondamental du système tandis que l'hamiltonien est varié à celui du problème, en utilisant le tunneling pour rester près de l'état fondamental comme décrit dans la réponse de Nat .

Maintenant, pourquoi cela ne peut-il pas être utilisé pour décrire un modèle de porte QC? Ce qui précède est un problème d' optimisation binaire non contraint quadratique (QUBO) , qui est NP-difficile ... En effet, voici un article mappant un certain nombre de problèmes NP au modèle Ising . Tout problème dans NP peut être mappé à n'importe quel problème NP-dur en temps polynomial et la factorisation entière est en effet un problème NP.

Eh bien, la température n'est pas nulle, donc elle ne sera pas à l'état fondamental tout au long du recuit et, par conséquent, la solution n'est encore qu'approximative. Ou, en termes différents, la probabilité d'échec est supérieure à la moitié (c'est loin d'avoir une probabilité de réussite décente par rapport à ce qu'un CQ universel considère comme `` décent '' - à en juger par les graphiques que j'ai vus, la probabilité de succès pour le la machine actuelle est d'environ et cela ne fera qu'empirer avec l'augmentation de la taille), et l'algorithme de recuit n'est pas une erreur bornée. Du tout. En tant que tel, il n'y a aucun moyen de savoir si vous avez ou non la bonne solution avec quelque chose comme la factorisation entière.$0.2\%$

Ce qu'il fait (en principe), c'est se rapprocher très rapidement du résultat exact, mais cela n'aide en rien pour quoi le résultat exact est requis, car passer de «presque correct» à «correct» est toujours extrêmement difficile ( c'est-à-dire vraisemblablement toujours NP en général, quand le problème d'origine est dans NP) problème dans ce cas, car les paramètres qui sont / donnent une solution "presque correcte" ne vont pas nécessairement être distribués n'importe où près des paramètres qui sont / donnent le bonne solution.

Modifier pour clarification: ce que cela signifie, c'est qu'un recuit quantique (QA) prend toujours du temps exponentiel (bien que potentiellement un temps exponentiel plus rapide) pour résoudre des problèmes NP tels que la factorisation entière, où un QC universel donne une vitesse exponentielle et peut résoudre le même problème en temps poly. C'est ce qui implique qu'un QA ne peut pas simuler un QC universel en temps poly (sinon il pourrait résoudre des problèmes en temps poly qu'il ne peut pas). Comme indiqué dans les commentaires, ce n'est pas la même chose que de dire qu'un contrôle qualité ne peut pas donner la même accélération dans d'autres problèmes, tels que la recherche dans la base de données.

Le recuit est plus une tactique analogique.

L'essentiel est que vous avez une fonction étrange que vous souhaitez optimiser. Donc, vous rebondissez autour d'elle. Au début, la " température " est très élevée, de sorte que le point sélectionné peut beaucoup rebondir. Alors que l'algorithme " refroidit ", la température baisse et le rebond devient moins agressif.

En fin de compte, il s'installe à un optima local qui, idéalement, est favorablement comme l'opta global.

Voici une animation pour un recuit simulé (non quantique):

Mais, c'est à peu près le même concept pour le recuit quantique :

En revanche, la logique de porte est beaucoup plus numérique qu'analogique. Il s'agit de qubits et d'opérations logiques plutôt que de simplement trouver un résultat après un rebond chaotique.