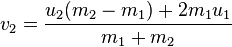Avec l'aide de la communauté Stack Overflow, j'ai écrit un simulateur de physique assez basique mais amusant.
Vous cliquez et faites glisser la souris pour lancer une balle. Il rebondira et finira par s'arrêter sur le "sol".
Ma prochaine grande fonctionnalité que je veux ajouter est la collision balle à balle. Le mouvement de la balle est divisé en un vecteur de vitesse ax et y. J'ai la gravité (petite réduction du vecteur y à chaque pas), j'ai le frottement (petite réduction des deux vecteurs à chaque collision avec un mur). Les balles se déplacent honnêtement d'une manière étonnamment réaliste.
Je suppose que ma question comporte deux parties:
- Quelle est la meilleure méthode pour détecter une collision balle à balle?
Ai-je juste une boucle O (n ^ 2) qui itère sur chaque balle et vérifie toutes les autres billes pour voir si son rayon se chevauche? - Quelles équations dois-je utiliser pour gérer les collisions de balle à balle? Physique 101
Comment affecte- t-il les vecteurs x / y de vitesse des deux balles? Quelle est la direction résultante dans laquelle les deux balles se dirigent? Comment appliquer cela à chaque balle?

La gestion de la détection de collision des «murs» et des changements de vecteur qui en ont résulté a été facile, mais je vois plus de complications avec les collisions boule-balle. Avec les murs, je devais simplement prendre le négatif du vecteur x ou y approprié et il irait dans la bonne direction. Avec des balles, je ne pense pas que ce soit comme ça.
Quelques précisions rapides: pour plus de simplicité, je suis d'accord avec une collision parfaitement élastique pour l'instant, aussi toutes mes balles ont la même masse en ce moment, mais je pourrais changer cela à l'avenir.
Edit: Ressources que j'ai trouvées utiles
Physique de la balle 2D avec des vecteurs: Collisions bidimensionnelles sans trigonométrie.pdf
Exemple de détection de collision de balle 2D: Ajout de la détection de collision
Succès!
J'ai la détection de collision de balle et la réponse qui fonctionnent très bien!
Code pertinent:
Détection de collision:
for (int i = 0; i < ballCount; i++)
{
for (int j = i + 1; j < ballCount; j++)
{
if (balls[i].colliding(balls[j]))
{
balls[i].resolveCollision(balls[j]);
}
}
}
Cela vérifiera les collisions entre chaque balle mais sautera les contrôles redondants (si vous devez vérifier si la balle 1 entre en collision avec la balle 2, vous n'avez pas besoin de vérifier si la balle 2 entre en collision avec la balle 1. En outre, elle ignore la vérification des collisions avec elle-même. ).
Ensuite, dans ma classe de balle, j'ai mes méthodes colliding () et resolCollision ():
public boolean colliding(Ball ball)
{
float xd = position.getX() - ball.position.getX();
float yd = position.getY() - ball.position.getY();
float sumRadius = getRadius() + ball.getRadius();
float sqrRadius = sumRadius * sumRadius;
float distSqr = (xd * xd) + (yd * yd);
if (distSqr <= sqrRadius)
{
return true;
}
return false;
}
public void resolveCollision(Ball ball)
{
// get the mtd
Vector2d delta = (position.subtract(ball.position));
float d = delta.getLength();
// minimum translation distance to push balls apart after intersecting
Vector2d mtd = delta.multiply(((getRadius() + ball.getRadius())-d)/d);
// resolve intersection --
// inverse mass quantities
float im1 = 1 / getMass();
float im2 = 1 / ball.getMass();
// push-pull them apart based off their mass
position = position.add(mtd.multiply(im1 / (im1 + im2)));
ball.position = ball.position.subtract(mtd.multiply(im2 / (im1 + im2)));
// impact speed
Vector2d v = (this.velocity.subtract(ball.velocity));
float vn = v.dot(mtd.normalize());
// sphere intersecting but moving away from each other already
if (vn > 0.0f) return;
// collision impulse
float i = (-(1.0f + Constants.restitution) * vn) / (im1 + im2);
Vector2d impulse = mtd.normalize().multiply(i);
// change in momentum
this.velocity = this.velocity.add(impulse.multiply(im1));
ball.velocity = ball.velocity.subtract(impulse.multiply(im2));
}
Code source: source complète pour collisionneur de balle à balle.
Si quelqu'un a des suggestions pour améliorer ce simulateur de physique de base, faites-le moi savoir! Une chose que je n'ai pas encore ajoutée est l'élan angulaire afin que les balles roulent de manière plus réaliste. D'autres suggestions? Laissez un commentaire!
Vector2d impulse = mtd.multiply(i);doit être i * le vecteur mtd normalisé. Quelque chose comme:Vector2d impulse = mtd.normalize().multiply(i);