Comment transformer un cube en sphère?

J'essaie de créer une sphère quadruple basée sur un article , qui montre des résultats comme celui-ci:

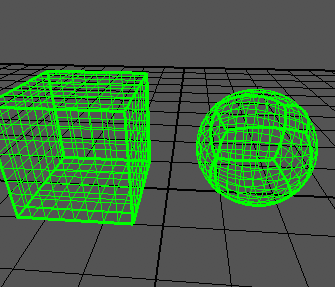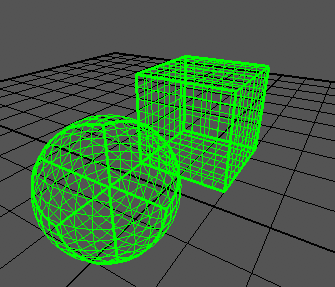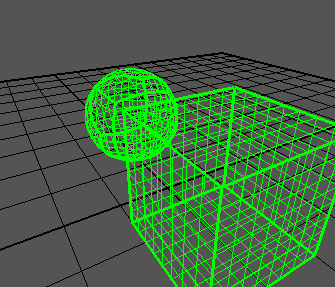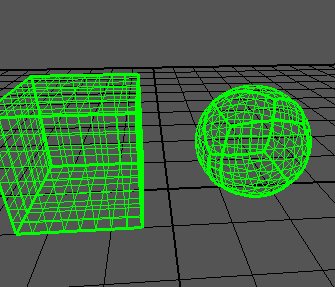
Je peux générer un cube correctement:

Mais quand je convertis tous les points selon cette formule (à partir de la page liée ci-dessus):

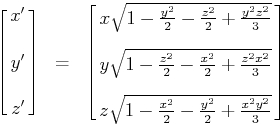
    x = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
    y = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
    z = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

Ma sphère ressemble à ceci:

Comme vous pouvez le voir, les bords du cube poussent encore trop loin. Le cube s'étend de -1à +1sur tous les axes, comme le dit l'article.

Des idées ce qui ne va pas?

Vous avez mal écrit la formule.

x = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
y = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
z = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

Vous modifiez l'original xet le remplacez. Ensuite, vous modifiez en yfonction non pas de l'original xmais du modifié x. Ensuite, vous modifiez en zfonction de la version modifiée des deux .

Conservez les originaux et calculez ceci:

float dx = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
float dy = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
float dz = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

Utilisez ensuite dx, dy et dz.