Bande passante de l'oscilloscope, de quoi s'agit-il?

Cette question m'est apparue il y a quelques instants. Je mesurais ce qui est censé être une onde carrée de 50 MHz de niveau 0 à 2,5, mais ce que j'ai vu à l'écran est une onde sinusoïdale centrée autour de 1,2 V et un niveau de 0,5 à 2,0 V, la fréquence était de 4 MHz.

J'ai vérifié ma fiche technique des oscilloscopes et elle a montré que la bande passante était de 10 MHz avec un taux d'échantillonnage de 50 MS / s.

Je me demande ce que sont ces chiffres.

• Sont-ils une mesure de la limite de fréquence supérieure qu'un oscilloscope peut mesurer?
• Cet oscilloscope est-il capable de mesurer 50 MHz à tous?

La bande passante du système est une combinaison de la bande passante de la sonde et de la bande passante d'entrée de l'oscilloscope. Chacun peut être approximé par un circuit passe-bas RC, ce qui signifie que les retards s'ajoutent géométriquement:

t_system^2 = (t_probe^2 + t_scope^2)
f_system = 1/sqrt((1/f_probe)^2 + (1/f_scope)^2)

Cela signifie qu'un oscilloscope à 10 MHz avec des sondes à 60 MHz peut mesurer des sinusoïdes de fréquence 9,86 MHz avec une atténuation de -3 dB (100 * 10 ^ {- 3/20}%).

Lors de la mesure des trains d'impulsions numériques, ce n'est pas tant la périodicité qui importe, mais les temps de montée et de descente, car ils contiennent les informations à haute fréquence. Les temps de montée peuvent être estimés mathématiquement par une élévation RC ou une élévation gaussienne, et sont définis comme le temps pour que le signal passe de 10% de la différence entre la basse tension (logique 0) et la haute tension (logique 1) , à 90% de la différence. Par exemple, dans un système 5V / 0V, il est défini comme le temps pour aller de 0.1*5V=0.5Và 0.9*5V=4.5V. Avec ces contraintes et quelques calculs fantaisistes , on peut comprendre que chaque type de temps de montée caractéristique a un contenu en fréquence jusqu'à environ 0.34/t_risepour gaussien et0.35/t_risepour RC. (J'utilise 0.35/t_risesans raison valable et je le ferai pour le reste de cette réponse.)

Ces informations fonctionnent également dans l'autre sens: une bande passante système particulière ne peut mesurer que les temps de montée jusqu'à 0.35/f_system; dans votre cas, 35 à 40 nanosecondes. Vous voyez quelque chose de similaire à une onde sinusoïdale, car c'est ce que le frontal analogique laisse passer.

Le crénelage est un artefact d'échantillonnage numérique, et est également en vigueur dans votre mesure (vous n'avez pas de chance!). Voici une image empruntée à WP:

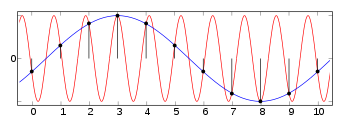
Comme le frontal analogique ne laisse passer que des temps de montée de 35 ns à 40 ns, le pont d'échantillonnage ADC voit quelque chose comme une onde sinusoïdale atténuée de 50 MHz, mais il n'échantillonne qu'à 50 ms / s, il ne peut donc lire que les sinusoïdes inférieures à 25 MHz. De nombreux oscilloscopes ont un filtre anti-crénelage (LPF) à ce stade, qui atténuerait les fréquences supérieures à 0,5 fois la fréquence d'échantillonnage (critères d'échantillonnage de Shannon-Nyquist). Votre portée ne semble pas avoir ce filtre, car la tension crête à crête est encore assez élevée. De quel modèle s'agit-il?

Après le pont d'échantillonnage, les données sont poussées dans quelques processus DSP, dont l'un est appelé décimation et plages cardinales , ce qui réduit davantage le taux d'échantillonnage et les bandes passantes afin de mieux les afficher et les analyser (particulièrement utile pour le calcul FFT). Les données sont encore massées de manière à ne pas afficher de fréquences supérieures à ~ 0,4 fois la fréquence d'échantillonnage, appelée bande de garde . Je m'attendais à ce que vous voyiez une sinusoïde ~ 20 MHz - avez-vous activé la moyenne (5 points)?

EDIT: Je vais sortir mon cou et deviner que votre oscilloscope a un antialiasing numérique, utilisant la décimation et les portées cardinales, ce qui signifie essentiellement un LPF numérique puis un rééchantillonnage d'un chemin interpolé. Le programme DSP voit un signal de 20 MHz, il le décime donc jusqu'à ce qu'il soit inférieur à 10 MHz. Pourquoi 4 MHz et pas plus proche de 10 MHz? "La portée cardinale" signifie la réduction de moitié de la bande passante, et la décimation est souvent également par une puissance de deux. Une puissance entière de 2 ou une simple fraction de celle-ci a provoqué une sinusoïde de 4 MHz crachée au lieu de ~ 20 MHz. C'est pourquoi je dis que chaque passionné a besoin d'une portée analogique. :)

_{EDIT2: Étant donné que cela obtient tant de vues, je ferais mieux de corriger la conclusion embarrassante ci-dessus.}
EDIT2: L'outil particulier que vous aimiez peut utiliser le sous-échantillonnage, pour lequel une entrée analogique BPF de fenêtrage est requise pour l'anticrénelage, que cet outil ne semble pas avoir, donc il ne doit avoir qu'un LPF, le limitant aux sinusoïdes de moins de 25 MHz même en utilisant équiv. échantillonnage temporel . Bien que je soupçonne également la qualité du côté analogique, le côté numérique ne fait probablement pas les algorithmes DSP susmentionnés, mais plutôt le streaming de données ou le transfert d'une captureà la fois pour le calcul du nombre de force brute sur un PC. 50 ms / s et des longueurs de mot de 8 bits signifient que cela génère ~ 48 Mo / s de données brutes - beaucoup trop pour être diffusées via USB malgré sa limite théorique de 60 Mo / s (la limite pratique est de 30 Mo / s-40 Mo / s), peu importe la surcharge de mise en paquets, donc il y a une décimation dès la sortie de la boîte pour réduire cela. Travailler avec 35 Mo / s donne un taux d'échantillonnage de ~ 37 MS / s, pointant vers une limite de mesure théorique de 18 MHz, ou un temps de montée de 20 ns, lors de la diffusion, bien qu'il soit probablement inférieur car 35 Mo / s est incroyable (mais possible!). Le manuel indique qu'il existe un mode de blocage pour la capture de données à 50 Mo / s jusqu'à la mémoire interne de 8 Ko (toux)est plein (160us), puis l'envoyer à l'ordinateur à un rythme tranquille. Je suppose que les difficultés rencontrées dans la conception d'une entrée analogique de qualité ont été partiellement surmontées par un suréchantillonnage de 2X (précision supplémentaire d'un demi-bit), donnant un taux d'échantillonnage effectif de 25 MS / s, une fréquence maximale de 12,5 MHz et une bande de garde de 10% ( (0.5*25-10)/25), qui pourraient tous être réduits dans l'outil à main lui-même. En conclusion, je ne sais pas pourquoi vous voyez une sinusoïde à 4 MHz car il existe des moyens pour que cela se produise, mais je voudrais faire la même mesure en mode bloc, puis analyser les données avec un programme tiers. _{J'ai toujours été dur avec les oscilloscopes basés sur PC, mais celui-ci semble avoir des entrées décentes ...}

Une bande passante analogique de 10 MHz signifie qu'un signal de 10 MHz à 10 V ressemblera à un 5 V, en d'autres termes, votre amplitude sera divisée par deux à 10 MHz.

La bande passante de 10 MHz signifie que votre signal de 50 MHz sera atténué un peu, mais combien il est difficile de spéculer.

Les 50 MS / s signifient que vous ne pouvez pas travailler de manière réaliste avec des signaux bien supérieurs à 5 MHz si vous espérez effectuer une capture en une seule fois du signal, ce qui est vraiment la seule raison d'avoir un DSO en premier lieu.

En ignorant le problème de bande passante pendant une minute, vous pourriez être en mesure de mettre l'oscilloscope en mode d'échantillonnage répétitif et de capturer un signal répétitif de cette façon, tout comme un oscilloscope analogique.

J'obtiendrais un DSO approprié (le Rigol ds1052e modded à 100 MHz de bande passante analogique obtient mes recommandations), à défaut qu'un oscilloscope analogique Tektronix utilisé soit une bonne façon de procéder (j'utilise de temps en temps les modèles 2236, 2246 et 2247A et ce sont tous de belles portées analogiques)

* Are they a measure of the upper frequency limit an oscilloscope can measure?

Oui pour une mesure directe.

* Is this oscilloscope capable of measuring 50Mhz at all?

Oui, en utilisant des méthodes délicates: 1) Détection de crête (utile lorsque vous devez voir un signal modulé AM) 2) Décalage de fréquence (encore une fois, utile lorsque le signal est modulé) - Si vous mélangez un signal de 50 MHz avec une onde sinusoïdale de 49 MHz, vous obtiendrez Signal 1Mhz près de la fréquence souhaitée.

La bande passante et la fréquence d'échantillonnage doivent normalement être de 4 à 5 fois la fréquence maximale que vous souhaitez mesurer. Mais sachez que si votre signal d'entrée n'est pas une onde sinusoïdale pure, comme dans votre cas l'onde carrée, il contient également des harmoniques avec des fréquences beaucoup plus élevées. Pour une mesure précise, vous devez couvrir au moins la première de ces harmoniques.

A la fréquence de la bande passante maximale (ici 10 MHz), une onde sinusoïdale de cette fréquence est atténuée de 3 dB par le frontend analogique de l'oscilloscope. Cela signifie qu'il est mesuré à seulement 70% de sa valeur réelle. La fréquence d'échantillonnage spécifie le nombre de mesures effectuées par l'oscilloscope par seconde, c'est-à-dire la précision de l'acquisition de la forme du signal (50 MS / s équivaut à 5 mesures par cycle sur un signal à 10 MHz).

Réfléchissez maintenant à ce que voit votre oscilloscope avec le signal d'entrée fortement atténué (en raison de la bande passante trop faible) et avec seulement 5 échantillons par cycle (en raison de la fréquence d'échantillonnage).