Chemin traçant le BRDF de Cook-Torrance

27

- Désolé pour le long post, mais je préfère le faire parce que "Le diable est dans les détails. " :)

J'écris un traceur de chemin à partir de zéro et il fonctionne bien pour les surfaces parfaitement diffuses (lambertiennes) ( c'est-à - dire que le test du four indique - au moins visuellement - qu'il est économe en énergie, et les images rendues correspondent à celles générées avec le rendu Mitsuba pour le même paramètres). Maintenant, j'implémente le support du terme spéculaire du modèle microfacet original de Cook-Torrance, afin de rendre certaines surfaces métalliques. Cependant, il semble que cette BRDF reflète plus d'énergie que celle reçue. Voir les exemples d'images ci-dessous:

Image ci-dessus: référence Mitsuba (supposée être correcte) image: traçage de chemin avec échantillonnage direct de la lumière, échantillonnage de l'hémisphère d'importance, longueur maximale du chemin = 5, 32 spp stratifiés, filtre carré, rugosité de surface = 0,2, RVB.

Image ci-dessus: Image réelle rendue: traçage de trajectoire naïve par force brute, échantillonnage uniforme de l'hémisphère, longueur maximale du trajet = 5, 4096 spp stratifiés, filtre carré, rugosité de surface = 0,2, RVB. Malgré quelques différences en ce qui concerne les paramètres de rendu, il est clair que l'image rendue ne convergera pas vers la référence indiquée précédemment.

J'ai tendance à penser que ce n'est pas un problème d'implémentation, mais un problème concernant la bonne utilisation du modèle Cook-Torrance dans le cadre de l'équation de rendu. Ci-dessous, j'explique comment j'évalue le BRDF spéculaire et je voudrais savoir si je le fais correctement et, sinon, pourquoi.

Avant d'entrer dans les détails, notez que le moteur de rendu est assez simple: 1) implémente uniquement l'algorithme de traçage de chemin naïf par force brute - pas d'échantillonnage de lumière directe, pas de traçage de chemin bidirectionnel, pas de MLT; 2) tout l'échantillonnage est uniforme sur l'hémisphère au-dessus du point d'intersection - aucun échantillonnage d'importance, ni pour les surfaces diffuses; 3) le trajet des rayons a une longueur maximale fixe de 5 - pas de roulette russe; 4) la radiance / réflectance est informée par des tuples RVB - aucun rendu spectral.

Modèle de microfacet Cook Torrance

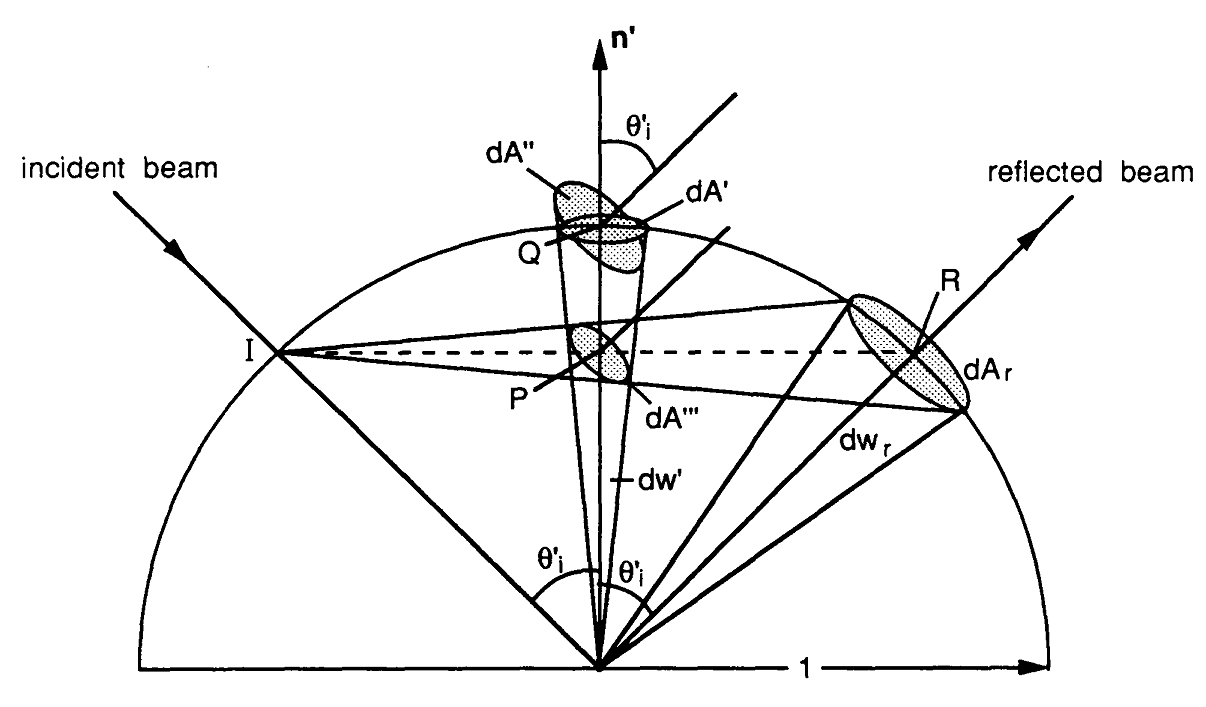
Maintenant, je vais essayer de construire le chemin que j'ai suivi pour implémenter l'expression d'évaluation BRDF spéculaire. Tout commence par l'équation de rendu où est le point d'intersection à la surface , est le vecteur de visualisation,

L_{o} (p, w_{o}) = L_{e} + \int_{Ω} L_{i} (p, w_{i}) f r (w_{o}, w_{i}) \cos θ d ω

$L_o(\textbf{p}, \mathbf{w_o}) = L_e + \int_{\Omega} L_i(\textbf{p}, \mathbf{w_i}) fr(\mathbf{w_o}, \mathbf{w_i}) \cos \theta d\omega$

p

$\textbf{p}$

w_{o}

$\mathbf{w_o}$

w_{i}

$\mathbf{w_i}$ est le vecteur lumineux,

est le rayonnement sortant le long de

,

est le rayonnement incident sur

long de

et

.

L_{o}

$L_o$

w_{o}

$\mathbf{w_o}$

L_{i}

$L_i$

p

$\textbf{p}$

w_{i}

$\mathbf{w_i}$

\cos θ = n \cdot w_{i}

$\cos \theta = \mathbf{n} \cdot \mathbf{w_i}$

L'intégrale ci-dessus ( c'est-à - dire le terme de réflexion de l'équation de rendu) peut être approximée avec l'estimateur de Monte Carlo suivant oùest la fonction de densité de probabilité (PDF) qui décrit la distribution des vecteurs d'échantillonnage.

\frac{1}{N} \sum_{k = 1}^{N} \frac{L_{i} (p, w_{k}) f r (w_{k}, w_{o}) \cos θ}{p (w_{k})}

$\frac{1}{N} \sum_{k=1}^{N} \frac{ L_i(\textbf{p}, \mathbf{w_k}) fr(\mathbf{w_k}, w_o) \cos \theta }{p(\mathbf{w_k})}$

p

$p$

w_{k}

$\mathbf{w_k}$

Pour le rendu réel, le BRDF et le PDF doivent être spécifiés. Dans le cas du terme spéculaire du modèle Cook-Torrance, j'utilise le BRDF suivant où

f r (w_{i}, w_{o}) = \frac{D F G}{π (n \cdot w_{i}) (n \cdot w_{o})}

$fr(\mathbf{w_i}, \mathbf{w_o}) = \frac{DFG}{\pi (\mathbf{n} \cdot \mathbf{w_i})(\mathbf{n} \cdot \mathbf{w_o})}$

D = \frac{1}{m^{2} (n \cdot h)^{4}} \exp (\frac{(n \cdot h)^{2} - 1}{m^{2} (n \cdot h)^{2}})

$D = \frac{1}{m^2 (\mathbf{n} \cdot \mathbf{h})^4} \exp \left( {\frac{(\mathbf{n} \cdot \mathbf{h})^2 - 1}{m^2 (\mathbf{n} \cdot \mathbf{h})^2}} \right)$

F = c_{s p e c} + (1 - c_{s p e c}) (1 - w_{i} \cdot h)^{5}

$F = c_{spec} + (1 - c_{spec}) (1 - \mathbf{w_i} \cdot \mathbf{h})^5$

Dans les équations ci-dessus,

G = min (1, \frac{2 (n \cdot h) (n \cdot w_{o})}{w_{o} \cdot h}, \frac{2 (n \cdot h) (n \cdot w_{i})}{w_{o} \cdot h})

$G = \min \left( 1, \frac{2(\mathbf{n} \cdot \mathbf{h})(\mathbf{n} \cdot \mathbf{w_o})}{\mathbf{w_o} \cdot \mathbf{h}}, \frac{2(\mathbf{n} \cdot \mathbf{h})(\mathbf{n} \cdot \mathbf{w_i})}{\mathbf{w_o} \cdot \mathbf{h}} \right)$

et

est la couleur spéculaire. Toutes les équations, à l'exception de

, ont été extraites de l'article original.

, également connu sous le nomd'approximation de Schlick, est uneapproximationefficace et moins précise du terme de Fresnel réel.

h = \frac{w_{o} + w_{i}}{| w_{o} + w_{i} |}

$\mathbf{h} = \frac{\mathbf{w_o} + \mathbf{w_i}}{|\mathbf{w_o} + \mathbf{w_i}|}$

c_{s p e c}

$c_{spec}$

F

$F$

F

$F$

$m \approx 0.2$

p (w_{k}) = \frac{1}{2 π}

$p(\mathbf{w_k}) = \frac{1}{2 \pi}$

w_{i}

$\mathbf{w_i}$

w_{k}

$\mathbf{w_k}$

\frac{1}{N} \sum_{k = 1}^{N} \frac{L_{i} (p, w_{k}) (\frac{D F G}{π (n \cdot w_{k}) (n \cdot w_{o})}) \cos θ}{(\frac{1}{2 π})}

$\frac{1}{N} \sum_{k=1}^{N} \frac{ L_i(\textbf{p}, \mathbf{w_k})\left( \frac{DFG}{\pi (\mathbf{n} \cdot \mathbf{w_k})(\mathbf{n} \cdot \mathbf{w_o})} \right) \cos \theta }{\left( \frac{1}{2\pi} \right)}$

π

$\pi$

2 L_{i} (p, w_{k}) (\frac{D F G}{(n \cdot w_{k}) (n \cdot w_{o})}) \cos θ

$2 L_i(\textbf{p}, \mathbf{w_k})\left( \frac{DFG}{(\mathbf{n} \cdot \mathbf{w_k})(\mathbf{n} \cdot \mathbf{w_o})} \right) \cos \theta$

\cos θ = n \cdot w_{k}

$\cos \theta = \mathbf{n} \cdot \mathbf{w_k}$

2 L_{i} (p, w_{k}) (\frac{D F G}{n \cdot w_{o}})

$2 L_i(\textbf{p}, \mathbf{w_k})\left( \frac{DFG}{\mathbf{n} \cdot \mathbf{w_o}} \right)$

C'est donc l'expression que j'évalue lorsqu'un rayon frappe une surface spéculaire dont la réflectance est décrite par le BRDF de Cook-Torrance. C'est l'expression qui semble refléter plus d'énergie que celle reçue. Je suis presque sûr qu'il y a quelque chose qui ne va pas (ou dans le processus de dérivation), mais je ne le vois pas.

$\frac{1}{\pi}$

Toute aide est la bienvenue! Merci!

MISE À JOUR

$D$ $\frac{1}{\pi}$ $fr$ $\frac{1}{4}$

D_{n e w} = \frac{1}{π m^{2} (n \cdot h)^{4}} \exp (\frac{(n \cdot h)^{2} - 1}{m^{2} (n \cdot h)^{2}})

$D_{new} = \frac{1}{\pi m^2 (\mathbf{n} \cdot \mathbf{h})^4} \exp \left( {\frac{(\mathbf{n} \cdot \mathbf{h})^2 - 1}{m^2 (\mathbf{n} \cdot \mathbf{h})^2}} \right)$

f r_{n e w} (w_{i}, w_{o}) = \frac{D F G}{4 (n \cdot w_{i}) (n \cdot w_{o})}

$fr_{new}(\mathbf{w_i}, \mathbf{w_o}) = \frac{DFG}{4 (\mathbf{n} \cdot \mathbf{w_i})(\mathbf{n} \cdot \mathbf{w_o})}$

\frac{π}{2} L_{i} (p, w_{k}) (\frac{D_{n e w} F G}{n \cdot w_{o}})

$\frac{\pi}{2} L_i(\textbf{p}, \mathbf{w_k})\left( \frac{D_{new}FG}{\mathbf{n} \cdot \mathbf{w_o}} \right)$

D

$D$

f r

$fr$

MISE À JOUR 2

Comme l'a souligné PeteUK , la paternité de la formulation de Fresnel présentée dans le texte original de ma question a été attribuée à tort à Cook et Torrance. La formulation de Fresnel utilisée ci-dessus est en fait connue comme l' approximation de Schlick et porte le nom de Christophe Schlick. Le texte original de la question a été modifié en conséquence.

— Christian Pagot
source

Je ne sais pas si vous visitez toujours ce site, mais j'ai une question concernant votre équation de Fresnel et je l'ai postée ici

— PeteUK

12

$\frac{1}{\pi}$ $f_r$ $\frac{1}{4}$

f_{r} = \frac{D F G}{4 (n \cdot w_{i}) (n \cdot w_{o})},

$f_r = \frac{DFG}{4(n\cdot w_i)(n \cdot w_o)},$

\frac{π}{2} L_{i} (p, w_{k}) (\frac{D F G}{n \cdot w_{o}}) .

$\frac{\pi}{2}L_i(p,w_k)\left(\frac{DFG}{n\cdot w_o}\right).$

— wolle
source

\frac{1}{4}

$\frac{1}{4}$

\frac{1}{π}

$\frac{1}{\pi}$

= \frac{π}{2}

$= \frac{\pi}{2}$

1 / π

$1/\pi$

\frac{1}{π}

$\frac{1}{\pi}$

D

$D$

\frac{1}{4}

$\frac{1}{4}$

f_{r}

$f_r$

\frac{1}{π}

$\frac{1}{\pi}$

D

$D$

π

$\pi$

\frac{1}{π}

$\frac{1}{\pi}$

D

$D$

\frac{1}{4}

$\frac{1}{4}$

f r

$fr$

13

$\frac{1}{\pi}$ $\frac{1}{4}$

$\frac{1}{\pi}$

$\frac{1}{4(n \cdot \omega_i)}$

$\frac{1}{4}$

Pour une belle explication du terme, vous devriez vérifier [Nayar, 91] , annexe D. Voici une image du même papier:

d ω^{'} = \frac{d ω_{r}}{4 \cos θ_{i}^{'}}

$d\omega' = \frac{d\omega_r}{4\cos{\theta_i'}}$

$\frac{1}{4}$

— Samu
source