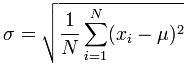C ++ 14, 340 383 octets
En tant que lambda générique sans nom. Le premier paramètre Lest la liste std::listdu type à virgule flottante et le deuxième paramètre est le flux de sortie souhaité, comme std::cout.
#import<cmath>
#define F(x);O<<x<<'\n';
#define Y l=k;++l!=L.end();
#define A auto
[](A L,A&O){A S=L;A l=L.begin(),k=l;A n=L.size();A s=*l,p=s,d=s*s,h=n/2.;for(S.sort(),Y s+=*l,p*=*l,d+=*l**l);for(l=S.begin();--h>0;++l)F(s)F(p)F(s/n)F(*l)for(Y)O<<*l-*k++<<","F(' ')for(A x:S)O<<x<<","F(' ')F(S.front())F(S.back())F(sqrt((d-s*s/n)/(n-1)))}
Compile avec un avertissement, C ++ ne permet pas "directement suivi par des littéraux comme F. Le programme est toujours en cours d'exécution.
- -1 & -2 octets grâce à Zacharý
Non golfé:
#include<iostream>
#include<list>
#import<cmath>
#define F(x);O<<x<<'\n';
#define Y l=k;++l!=L.end();
#define A auto
auto f=
[](A L, A&O){
A S=L; //copy the list for later sorting
A l=L.begin(), //main iterator
k=l; //sidekick iterator
A n=L.size();
A s=*l, //sum, init with head of list
p=s, //product, same
d=s*s, //standard deviation, formula see https://en.wikipedia.org/wiki/Algebraic_formula_for_the_variance
h=n/2.; //for the median later
for(
S.sort(), //now min/med/max is at known positions in S
Y //l=k;++l!=L.end(); //skip the headitem-loop
s += *l, //l points the next element which is fine
p *= *l, //since the head given at definiten
d += *l * *l //needs the sum of the squares
);
for(
l=S.begin(); //std::list has no random access
--h>0; //that's why single increment loop
++l //until median is crossed
)
F(s) //;O<<s<<'\n'; //sum
F(p) //product
F(s/n) //average
F(*l) //median (in S)
for(Y) //l=k;++l!=L.end(); //set l back to L
O<<*l-*k++<<"," //calc difference on the fly
F(' ')
for(A x:S) //output sorted list
O<<x<<","
F(' ')
F(S.front()) //minimum
F(S.back()) //maximum
F(sqrt((d-s*s/n)/(n-1))) //standard deviation
}
;
using namespace std;
int main() {
list<double> l = {10,3,1,2,4};
f(l, cout);
}