Si vous habitiez de l'autre côté de la Lune, comment pourriez-vous en déduire l'existence de la Terre?

Supposons que vous déposiez un astronome, armé de nos connaissances actuelles en mécanique orbitale, sur un dôme situé de l'autre côté de la Lune, afin que la Terre leur soit perpétuellement cachée.

(Et, bien sûr, supposons que cette personne n’a pas de connaissances spécifiques sur le système dans lequel elle se trouve, au-delà de ce qu’elle peut extraire des observations. Si vous voulez, imaginez qu’elle a appris toute notre mécanique orbitale moderne et la physique associée en alpha centauri, et puis s'est téléporté sur notre lune.)

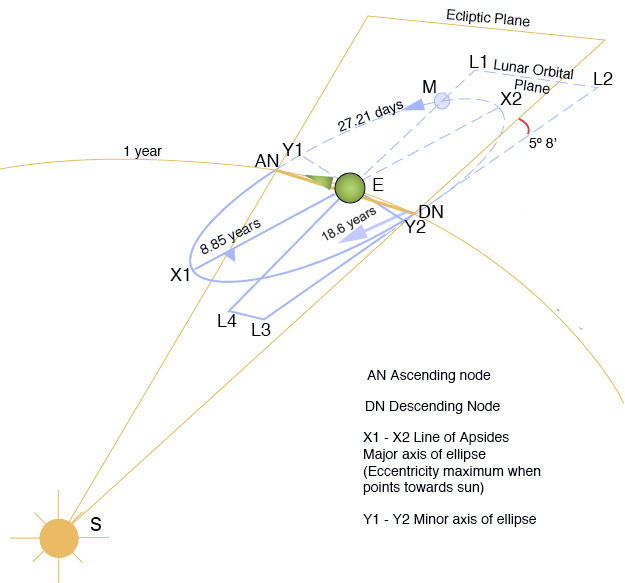
Or, il est raisonnable de s’attendre à ce que cette personne puisse déduire d’observations du ciel que le corps sur lequel elle se trouve est la moitié d’un système binaire et qu’elle devrait pouvoir mesurer les caractéristiques orbitales (demi-grand axe, l'ellipticité, l'inclination) ainsi que la position du barycentre (beaucoup plus proche de l'autre organe, correspondant à un partenaire beaucoup plus massif). Quelles observations faut-il en déduire? Quel niveau de précision d'observation est nécessaire pour ces observations et à quelle époque historique correspond-il? (Par exemple, l'équipement de Tycho Brahe aurait-il été suffisant? Celui de Galilée? Les anciens Grecs? Ou aurait-il besoin d'un observatoire de la fin du XIXe siècle (ou même plus tard?)?)

(Comme indiqué dans la réponse de MartinV, notre astronome pourrait avoir du mal à distinguer les situations avec une paire en orbite versus un seul corps énorme. Ainsi, si cela vous convient, vous pouvez supposer que, via de courtes incursions d'environ 100 km du dôme, notre astronome est: capable de mesurer le rayon lunaire en mesurant les inclinaisons solaires en différents points avec des distances connues entre eux, à la Erathostenes .)

— Emilio Pisanty
source

La parallaxe stellaire aiderait définitivement un long chemin, et c'est le 19ème siècle.

@ LucJ.Bourhis La parallaxe stellaire, ou du moins son composant principal, correspond au rayon orbital autour du Soleil, et les composants en orbite lunaire seraient beaucoup plus petits que cela, ce qui me semble une solution non évidente (et Il n’est pas évident non plus que les observations du 19ème siècle apporteraient la précision nécessaire). Je suppose que le candidat le plus probable est la parallaxe du Soleil sur l'arrière-plan stellaire (ou, de manière équivalente, des positions des étoiles par rapport à une horloge synchronisée avec le jour lunaire), mais j'aimerais savoir quelle précision (par rapport aux références historiques) vous D besoin de ça.

— Emilio Pisanty

Sûr! Ce n'est pas ce que j'avais en tête. Historiquement, le fait que la Lune soit observable depuis la Terre a joué un rôle déterminant dans la mesure de la distance Terre-Soleil à partir de laquelle beaucoup dépend de la distance. Je pensais utiliser la parallaxe pour avoir une poignée sur cette distance.

Néanmoins, la parallaxe d'un demi-mois pourrait être utile pour quelque chose comme Mars. Le diamètre orbital de la Lune est de ~ 0,0026 UA, Mars peut être de ~ 1AU, de sorte que cet angle est de ~ 0,0052 radian ou 0,3 degré, non? Vous ne savez pas exactement comment celles-ci se comparent aux observations de parallaxe stellaire au fil des ans, mais il semble que cela pourrait modifier de manière observable la position de Mars par rapport aux étoiles lointaines.

Je me demande si l'inclinaison de la Lune à 5 degrés serait suffisante. (5,14 degrés), ce qui correspond à environ 9% de la distance orbitale de haut en bas tous les 29 jours) ou 1 / 6e de 1 degré par rapport au soleil. Par rapport à Mars sur la passe rapprochée, un peu moins. 14 jours d’observation du mouvement vers le haut ou du bas de Mars, mais pas de manière constante, car, parfois, vers le haut, parfois vers le bas, cela pourrait être le plus perceptible.

— userLTK

Réponses:

Un sismomètre de marée corporelle situé de l'autre côté de la lune détecterait à la fois la marée solaire et la distorsion corporelle de 20 pouces produite par la Terre . Bien qu’elle soit "verrouillée", la lune n’est pas dans une orbite parfaitement circulaire et vacille également un peu; libration . Votre sismomètre devrait détecter les deux effets.

Regarder la parallaxe du cycle de mars tous les 28 jours, comme suggéré dans les commentaires ci-dessus, pourrait être un moyen plus simple.

— Wayfaring Stranger
source

C'est une réponse intéressante. La Terre soulèvera en effet une petite "marée" sur la Lune et la libration la fera bouger. L'effet est petit et subtil - permettrait-il à lui seul, en génie scientifique, de déduire l'existence d'un corps inconnu et invisible dans l'espace?

— MartinV

Les effets sismiques sont intéressants, bien que je ne sache pas comment les mesurer. Et oui, je conviens que la parallaxe est la réponse la plus probable, mais je cherchais quelque chose de plus quantitatif et détaillé.

— Emilio Pisanty

C'est une très bonne question - et assez subtile.

TL; DR;

L'opportunité la plus précoce pourrait être que des changements inter-mensuels de la parallaxe stellaire du Soleil pourraient amener l'observateur à conclure que soit i) la Lune est un corps unique, de très grande taille, en rotation, soit système rotatif. Cependant, i) semblerait être incompatible avec un horizon proche et fortement incurvé.

Sinon, certainement lorsque nous développerons un modèle quantitatif de la mécanique orbitale impliquant la masse et la gravité

Je ne pense pas que la parallaxe stellaire nous aiderait directement, car elle (à notre époque) nous dit simplement que nous sommes en orbite autour du soleil et que nous ne parlons guère du système Terre-Lune lui-même.

Voyons comment un équivalent de Ptolémée sur la Lune (appelez-le Lune-Ptolémée) pourrait le voir. Il n'aurait aucun moyen de distinguer le système Terre-Lune de son hypothèse qu'il est simplement assis sur un objet solide au centre de la création. Bien sûr, il ne verrait pas de "lune" en orbite autour de lui, mais il verrait le soleil, les étoiles et les grandes planètes. Une parallaxe stellaire (pour lui, le Soleil "se déplaçant à travers le zodiaque) lui dirait simplement que le Soleil tourne autour de sa Lune, tout comme les planètes. L'existence d'épicycles planétaires serait une curiosité nécessaire pour faire fonctionner son modèle - mais travailler et il n'a aucune notion de la Terre

Moon-Galileo pourrait (ou ne pourrait pas) être capable de développer le modèle héliocentrique - il manque une idée clé de Terre-Galilée: la Terre n'était pas spéciale parce que d'autres planètes avaient aussi des lunes. Moon-Galileo trouverait le système orbital de Jupiter intéressant, mais ce n’était pas une idée clé. Il se peut qu’il ne développe pas le nouveau modèle. Malgré tout, quelqu'un d'autre le ferait.

Néanmoins, dans un monde scientifique qualitatif, rien ne pourrait aider l’observateur de la Lune à déduire l’existence de la Terre derrière l’horizon.

Je pense que la vérité deviendrait inévitable lorsque la mécanique orbitale se serait suffisamment développée pour incorporer la masse et la gravité dans les calculs. C'était peut-être à l'époque de Moon-Kepler.

Je ne suis pas sûr d’être d’accord avec les commentaires concernant les observations des planètes - je ne vois pas en quoi elles permettent de distinguer un système Terre-Lune d’un corps de Lune en rotation très grand et simple sans co-orbiteur ( ce qui serait une hypothèse naturelle à faire). Même les changements mensuels de parallaxe causés par la rotation de la Lune autour de la Terre pourraient être évités en suggérant la simple rotation d'un corps de Lune beaucoup plus grand - bien que notre héros puisse certainement en douter de la compatibilité avec la courbure apparente et la distance qui les sépare. Horizon de la lune.

— MartinV
source

Il semble que j'ai mal compris l'intention de la question. Vous pouvez assumer la connaissance moderne complète de la mécanique orbitale, si nécessaire. Lors de comparaisons historiques, je m'intéresse principalement à la technique expérimentale et non aux avancées conceptuelles. Si vous préférez, vous pouvez penser à la situation en tant qu'astronome qui a appris toute la mécanique orbitale moderne sur l'alpha centauri, puis s'est téléporté à la surface de notre lune. Ils connaissent donc parfaitement le fonctionnement de la gravité et de la mécanique et n'ont aucune connaissance préalable du système spécifique dans lequel ils sont

— installés

Mais pour ce qui est de votre lune-Ptolémée, n'aurait-il pas besoin d'inclure un épicycle pour le soleil? C'est l'observation de la parallaxe stellaire qui serait traduite dans le rayon orbital Terre-Lune une fois que vous passerez à une perspective héliocentrique. Mais à quel point serait-il important et difficile à mesurer?

— Emilio Pisanty

Merci Emilio - sur l’épicycle solaire, je pense que ce serait probablement trop petit étant donné l’équipement disponible pour Moon-Ptolemy. Sur votre autre commentaire - pas de mauvaise communication du tout; c'était votre question, alors je pense avoir mal compris! Avec un expert avec un équipement moderne greffé sur la Lune, je pense qu’ils comprendraient cela assez rapidement - une combinaison des oscillations de la parallaxe combinées à la taille apparente de la Lune soulèverait certainement la question. En fait, l'expert examinerait la petite Lune rocheuse elle-même et poserait immédiatement la question "Quelle est cette orbite autour?"

— MartinV

Oui, je m'attends à ce qu'ils y parviennent rapidement. la question était de savoir comment et de quel équipement ils auraient besoin. (Sur votre dernière phrase, je ne pense pas que ce soit une pré-attente naturelle, étant donné que nous en savons très peu sur la prévalence des exoplanètes rocheuses. Mais rien qu'en regardant à la surface, les différences entre la Lune et Cérès sont minimes. La surface ne suggère donc pas nécessairement que vous êtes sur un satellite, mais compte tenu du rayon et de la gravité de la surface, la surface rocheuse et le manque d'atmosphère pourraient être des caractéristiques tout à fait naturelles.)

— Emilio Pisanty

Un observateur situé de l'autre côté de la lune aurait du mal à expliquer qu'il se trouve sur une seule planète à cause du mouvement de la chose la plus remarquable dans le ciel: le soleil!

En effet, en raison de l'excentricité de l'orbite de la lune autour de la Terre, la durée du jour, c'est-à-dire la "vitesse du soleil dans le ciel", dépend de votre position dans votre orbite lunaire.

Et à partir d'observations qu'elle peut faire, par exemple sur d'autres planètes presque parfaitement arrondies dans le système solaire (et pour des raisons bien connues), elle devrait être obligée d'écarter l'hypothèse "je me tiens debout sur un corps céleste elliptique célibataire".

Désolé, je ne peux pas calculer la variation de la durée du jour de l'autre côté de la lune dans un laps de temps raisonnable.

Un autre effet que je vais essayer d'illustrer avec des images de Wikipedia: l'élévation de la trajectoire du soleil dans le ciel changerait d'année en année (cycle: entre 8 et 9 années terriennes), en raison de la précession absidiale de la lune et de son plan en orbite incliné:

Par Rfassbind - Travail personnel., Domaine public, Lien

Par le géologue, Homunculus 2 - depuis Wikipedia anglais, CC BY 3.0 , Lien

— J. Chomel
source